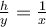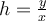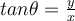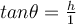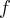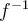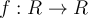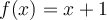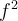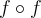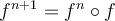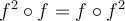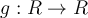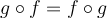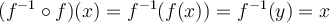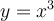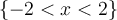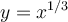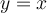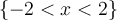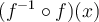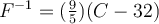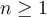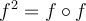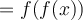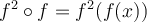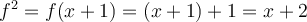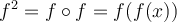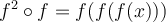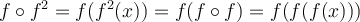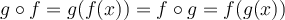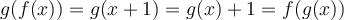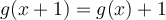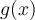What happens if we graph both 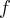 and
and 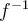 on the same set of axes, using the x-axis for the input to both
on the same set of axes, using the x-axis for the input to both 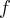 and
and 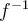 ?
?
Suppose 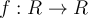 is a function from the set of real numbers to the same set with
is a function from the set of real numbers to the same set with 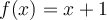 . We write
. We write 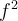 to represent
to represent 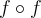 and
and 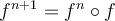 . Is it true that
. Is it true that 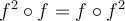 ? Why? Is the set {
? Why? Is the set {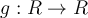 l
l 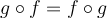 } infinite? Why?
} infinite? Why?
Inherently, the range of a function f (x) is the domain of the inverse function 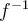 . The domain of
. The domain of 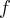 is the range of
is the range of 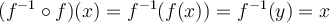 . So, what happens if we graph both
. So, what happens if we graph both 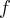 and
and 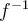 on the same set of axes, using the x-axis for the input to both
on the same set of axes, using the x-axis for the input to both 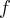 and
and 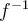 ? Let's try some examples.
? Let's try some examples.
If we type 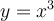
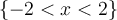 ,
, 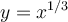
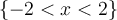 , and
, and 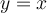
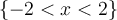 on the graph, all of the three functions will be limited in the same input
on the graph, all of the three functions will be limited in the same input 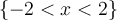 and their output will also affected by such a input boundary. The domain of
and their output will also affected by such a input boundary. The domain of 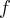 become the domain of
become the domain of 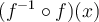 , not its range.
, not its range.
Let's try another example: C° to F°: Celsius to Fahrenheit Conversion Formula

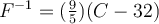
Again, as we can see that these these three lines are more like projections of each other from different angles rather than reflection.
The difficulty of setting the same set of axes for 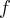 and
and 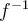 is that
is that 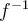 will become not fully or true inverse function of
will become not fully or true inverse function of 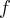 since the output of
since the output of 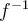 is limited. Instead of setting the input {-100 < x < 100}, the input of
is limited. Instead of setting the input {-100 < x < 100}, the input of 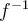 should be the range of
should be the range of 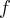
Suppose 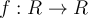 is a function from the set of real numbers to the same set with
is a function from the set of real numbers to the same set with 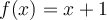 . We write
. We write 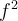 to represent
to represent 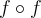 and
and 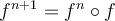 .
.
When 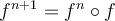 . and
. and 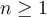
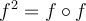
If 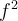 represents
represents 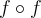
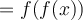 ,
, 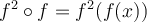
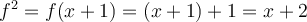
It is similar to an arithmetic progression which the next one is the previous number +1
Recall that 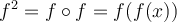
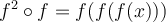
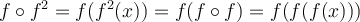
Therefore, 
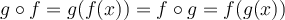
In this case, 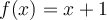
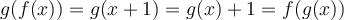
Now, we know that the set has to satisfy the equation 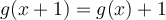
If the domain of 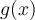 is all real numbers, then g(1)=g(0)+1, g(2)=g(1)+1, g(3)=g(2)+1,....... it will be infinite.
is all real numbers, then g(1)=g(0)+1, g(2)=g(1)+1, g(3)=g(2)+1,....... it will be infinite.
![(1+ \sqrt[]{3}i)^3 (1+ \sqrt[]{3}i)^3](https://my.uopeople.edu/filter/tex/pix.php/e2a1aa6d30a021d4041e05b48fbfd819.png)
![r= \sqrt[]{ 1^{2}+( \sqrt[]{3})^2 } =2 r= \sqrt[]{ 1^{2}+( \sqrt[]{3})^2 } =2](https://my.uopeople.edu/filter/tex/pix.php/27e227ed3f7354581e815bbd29ef736c.png)
![tan \theta= \sqrt[]{3} tan \theta= \sqrt[]{3}](https://my.uopeople.edu/filter/tex/pix.php/fbaaa49376a34eac20e70354b2af50f2.png)
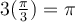
![(1+ \sqrt[]{3}i)^3=2^3(cos\pi +sin \pi)=-8 (1+ \sqrt[]{3}i)^3=2^3(cos\pi +sin \pi)=-8](https://my.uopeople.edu/filter/tex/pix.php/1655edd02ce67ad8bf191b7f102e190b.png)
![(\sqrt[]{2}+ \sqrt[]{2}i)^3 (\sqrt[]{2}+ \sqrt[]{2}i)^3](https://my.uopeople.edu/filter/tex/pix.php/5244302c0513b4819db33055eb6006d4.png)
![r= \sqrt[]{ (\sqrt[]{2})^{2}+( \sqrt[]{2})^2 } =2 r= \sqrt[]{ (\sqrt[]{2})^{2}+( \sqrt[]{2})^2 } =2](https://my.uopeople.edu/filter/tex/pix.php/e7ea7073eb6dfd20d2e687675801f89c.png)
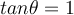
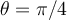
![(\sqrt[]{2}+ \sqrt[]{2}i)^3=2^3(cos3\pi/4 +sin3\pi/4)=\sqrt[]{2}(-4+4i) (\sqrt[]{2}+ \sqrt[]{2}i)^3=2^3(cos3\pi/4 +sin3\pi/4)=\sqrt[]{2}(-4+4i)](https://my.uopeople.edu/filter/tex/pix.php/27fa86cc1df32ea30b7bb303ec26f482.png)
![(1+ \sqrt[]{3}i)^{ \frac{1}{2}} (1+ \sqrt[]{3}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/0bcf834417249adadad03ab63b80f781.png)
![r= \sqrt[]{(1)^2+ (\sqrt[]{3})^2 } =2 r= \sqrt[]{(1)^2+ (\sqrt[]{3})^2 } =2](https://my.uopeople.edu/filter/tex/pix.php/b6c6ab4a7d3b72a4e501344b3878d9b4.png)
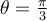
![(1+ \sqrt[]{3}i)^{ \frac{1}{2}} (1+ \sqrt[]{3}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/bc652a167de562231e4bfc6650ced7c8.png)
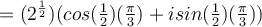
![\sqrt[]{2} ( \frac{\sqrt[]{3}}{2} + \frac{1}{2} i) \sqrt[]{2} ( \frac{\sqrt[]{3}}{2} + \frac{1}{2} i)](https://my.uopeople.edu/filter/tex/pix.php/05204267c26b6e10307752acfdad22f2.png)
![(\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}} (\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/c683ac0c2924fca4c2c086cb12a6ccc0.png)
![r= \sqrt[]{( \sqrt[]{2})^2+(\sqrt[]{2})^2} =2 r= \sqrt[]{( \sqrt[]{2})^2+(\sqrt[]{2})^2} =2](https://my.uopeople.edu/filter/tex/pix.php/e4ce902d69d67877998263642c396dfd.png)
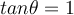
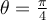
![(\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}} (\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/39deff4f37e68a7f4336999997dfcc1d.png)
![= \sqrt[]{2}(cos \frac{ \pi }{8} +isin \frac{ \pi }{8})= \sqrt[]{2}( \sqrt[]{\frac{1+ \frac{\sqrt[]{2}}{2} }{2} } +\sqrt[]{\frac{2-\sqrt[]{2} }{2} }) = \sqrt[]{2}(cos \frac{ \pi }{8} +isin \frac{ \pi }{8})= \sqrt[]{2}( \sqrt[]{\frac{1+ \frac{\sqrt[]{2}}{2} }{2} } +\sqrt[]{\frac{2-\sqrt[]{2} }{2} })](https://my.uopeople.edu/filter/tex/pix.php/1de22172a25f5ea46614d04c2f59681f.png)