One of the largest issues in ancient mathematics was accuracy—nobody had calculators that went out ten decimal places, and accuracy generally got worse as the numbers got larger. The famous Eratosthenes experiment, that can be found at https://www.famousscientists.org/eratosthenes/, relied on the fact known to Thales and others that a beam of parallels cut by a transverse straight line determines equal measure for the corresponding angles. Given two similar triangles, one with small measurements that can be accurately determined, and the other with large measurements, but at least one is known with accuracy, can the other two measurements be deduced? Explain and give an example.
The similarity of triangles gives rise to trigonometry.
How could we understand that the right triangles of trigonometry with a hypotenuse of measure 1 represent all possible right triangles? Ultimately, the similarity of triangles is the basis for proportions between sides of two triangles, and these proportions allow for the calculations of which we are speaking here. The similarity of triangles is the foundation of trigonometry.
Similar triangles are triangles that have the same shape, but their sizes may vary. If two triangles are similar, then their corresponding angles are congruent and corresponding sides are in equal proportion. Two triangles are similar if they have the same shape but are of different sizes. Thus mathematically, if two triangles are similar, then their corresponding sides are proportional and their corresponding angles are congruent.
Since these two triangles are similar triangles, 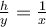 ,
, 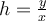
Reference
Abramson, J. (2017). Algebra and trigonometry. OpenStax, TX: Rice University. Retrieved from https://openstax.org/details/books/algebra-and-trigonometry
Admin. (2021, March 10). Similar triangles- Formula, Theorem & Proof of SSS, SAS AAA Similarity. BYJUS. Retrieved December 26, 2022, from https://byjus.com/maths/similar-triangles/


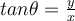
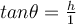



No comments:
Post a Comment
Note: Only a member of this blog may post a comment.