Finding powers of complex numbers is greatly simplified using De Moivre’s Theorem.
According to the De Moivre’s Theorem
If Z = r(cos θ + isin θ) is a complex number, then Zn = rn[cos(nθ) + isin(nθ)]
where n is a positive integer. Zn = rn cis(nθ)
How does it come from? To understand this theorem, we must know the products of complex numbers in polar form and the quotients of complex numbers in polar form first.
Recall that :
sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
sin(α – β) = sin(α)cos(β) – cos(α)sin(β)
cos(α + β) = cos(α)cos(β) – sin(α)sin(β)
cos(α – β) = cos(α)cos(β) + sin(α)sin(β)
![(1+ \sqrt[]{3}i)^3 (1+ \sqrt[]{3}i)^3](https://my.uopeople.edu/filter/tex/pix.php/e2a1aa6d30a021d4041e05b48fbfd819.png)
![r= \sqrt[]{ 1^{2}+( \sqrt[]{3})^2 } =2 r= \sqrt[]{ 1^{2}+( \sqrt[]{3})^2 } =2](https://my.uopeople.edu/filter/tex/pix.php/27e227ed3f7354581e815bbd29ef736c.png)
![tan \theta= \sqrt[]{3} tan \theta= \sqrt[]{3}](https://my.uopeople.edu/filter/tex/pix.php/fbaaa49376a34eac20e70354b2af50f2.png)
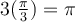
![(1+ \sqrt[]{3}i)^3=2^3(cos\pi +sin \pi)=-8 (1+ \sqrt[]{3}i)^3=2^3(cos\pi +sin \pi)=-8](https://my.uopeople.edu/filter/tex/pix.php/1655edd02ce67ad8bf191b7f102e190b.png)
![(\sqrt[]{2}+ \sqrt[]{2}i)^3 (\sqrt[]{2}+ \sqrt[]{2}i)^3](https://my.uopeople.edu/filter/tex/pix.php/5244302c0513b4819db33055eb6006d4.png)
![r= \sqrt[]{ (\sqrt[]{2})^{2}+( \sqrt[]{2})^2 } =2 r= \sqrt[]{ (\sqrt[]{2})^{2}+( \sqrt[]{2})^2 } =2](https://my.uopeople.edu/filter/tex/pix.php/e7ea7073eb6dfd20d2e687675801f89c.png)
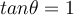
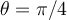
![(\sqrt[]{2}+ \sqrt[]{2}i)^3=2^3(cos3\pi/4 +sin3\pi/4)=\sqrt[]{2}(-4+4i) (\sqrt[]{2}+ \sqrt[]{2}i)^3=2^3(cos3\pi/4 +sin3\pi/4)=\sqrt[]{2}(-4+4i)](https://my.uopeople.edu/filter/tex/pix.php/27fa86cc1df32ea30b7bb303ec26f482.png)
![(1+ \sqrt[]{3}i)^{ \frac{1}{2}} (1+ \sqrt[]{3}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/0bcf834417249adadad03ab63b80f781.png)
![r= \sqrt[]{(1)^2+ (\sqrt[]{3})^2 } =2 r= \sqrt[]{(1)^2+ (\sqrt[]{3})^2 } =2](https://my.uopeople.edu/filter/tex/pix.php/b6c6ab4a7d3b72a4e501344b3878d9b4.png)
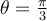
![(1+ \sqrt[]{3}i)^{ \frac{1}{2}} (1+ \sqrt[]{3}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/bc652a167de562231e4bfc6650ced7c8.png)
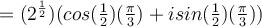
![\sqrt[]{2} ( \frac{\sqrt[]{3}}{2} + \frac{1}{2} i) \sqrt[]{2} ( \frac{\sqrt[]{3}}{2} + \frac{1}{2} i)](https://my.uopeople.edu/filter/tex/pix.php/05204267c26b6e10307752acfdad22f2.png)
![(\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}} (\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/c683ac0c2924fca4c2c086cb12a6ccc0.png)
![r= \sqrt[]{( \sqrt[]{2})^2+(\sqrt[]{2})^2} =2 r= \sqrt[]{( \sqrt[]{2})^2+(\sqrt[]{2})^2} =2](https://my.uopeople.edu/filter/tex/pix.php/e4ce902d69d67877998263642c396dfd.png)
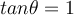
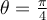
![(\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}} (\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/39deff4f37e68a7f4336999997dfcc1d.png)
![= \sqrt[]{2}(cos \frac{ \pi }{8} +isin \frac{ \pi }{8})= \sqrt[]{2}( \sqrt[]{\frac{1+ \frac{\sqrt[]{2}}{2} }{2} } +\sqrt[]{\frac{2-\sqrt[]{2} }{2} }) = \sqrt[]{2}(cos \frac{ \pi }{8} +isin \frac{ \pi }{8})= \sqrt[]{2}( \sqrt[]{\frac{1+ \frac{\sqrt[]{2}}{2} }{2} } +\sqrt[]{\frac{2-\sqrt[]{2} }{2} })](https://my.uopeople.edu/filter/tex/pix.php/1de22172a25f5ea46614d04c2f59681f.png)



No comments:
Post a Comment
Note: Only a member of this blog may post a comment.