What happen if we consider changes to the inside of a function? As the figure blow shows that when we multiply a function’s input by a positive constant, we get a function whose graph is stretched or compressed horizontally in relation to the graph of the original function. If the constant is between 0 and 1, we get a horizontal stretch; if the constant is greater than 1, we get a horizontal compression of the function.
Welcome to Intelligence Capitalism: The Techonomist's Edge. Here, we dive deep into the intersection of technology, artificial intelligence, and economic forces reshaping our world. Explore how innovation influences markets, society, and the future of capitalism, and gain insights into the complex dynamics driving today’s digital economy.
1/06/2023
Horizontal Stretches and Compressions of Functions
Vertical Stretches and Compression of Functions
When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. But why?
That's because each of the same input have been changed to the output 2x or o.5 of the original functions.
Reference
Abramson, J. (2017). Algebra and trigonometry. OpenStax, TX: Rice University. Retrieved from https://openstax.org/details/books/algebra-and-trigonometry
1/05/2023
Arc Length, Radius, Radians, and Trigonometric
1. Find the length of an arc in a circle of radius 10 centimeters subtended by the central angle of 50°
An arc length S is the length of the curve along the arc. Just as the full circumference of a circle always has a constant ratio to the radius, the arc length produced by any given angle also has a constant relation to the radius, regardless of the length of the radius. The radian measure is also depends only on the angle. A full revolution (360°) equals 2π radians. A half revolution (180°) is equivalent to π radians.
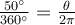
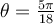
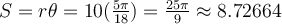
2. Graph 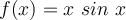 on [-4π, 4π] and verbalize how the graph varies from the graphs of
on [-4π, 4π] and verbalize how the graph varies from the graphs of 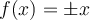 .
.
A function that has the same general shape as a sine or cosine function is known as a sinusoidal function. One of the general forms of sinusoidal functions is y = Asin(Bx − C) + D, where A represents its Amplitude, B represents its Periods, C and D represents its shifts. In this case, 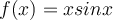 has only inconstant Amplitude X. Therefore, this function is expected to be a function that has the same period of
has only inconstant Amplitude X. Therefore, this function is expected to be a function that has the same period of 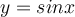 but with larger and larger Amplitudes. And, since the function
but with larger and larger Amplitudes. And, since the function 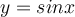 is repeating its values between the interval [-1, 1], when
is repeating its values between the interval [-1, 1], when 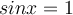 or
or 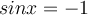 , the function
, the function 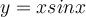 will repeatedly has the value of X and -X. In fact, they are the intersections of these functions,
will repeatedly has the value of X and -X. In fact, they are the intersections of these functions, 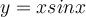 ,
, 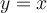 , and
, and 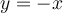
Graph 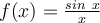 on the window [−5π, 5π] and describe freely what the graph shows.
on the window [−5π, 5π] and describe freely what the graph shows.
Similar to the previous sinusoidal functions. One of the general forms of sinusoidal functions is y = Asin(Bx − C) + D, where A represents its Amplitude, B represents its Periods, C and D represents its shifts. This time,
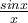 has only inconstant Amplitude
has only inconstant Amplitude 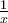 . Therefore, this function is expected to be a function that has the same period of
. Therefore, this function is expected to be a function that has the same period of 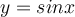 but with smaller and smaller Amplitudes. And, since the function
but with smaller and smaller Amplitudes. And, since the function 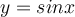 is repeating its values between the interval [-1, 1], when
is repeating its values between the interval [-1, 1], when 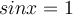 or
or 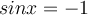 , the function
, the function 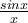 will repeatedly has the value of 1/X and -1/X. In fact, they are the intersections of these functions,
will repeatedly has the value of 1/X and -1/X. In fact, they are the intersections of these functions, 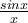 ,
, 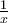 , and
, and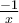
3. A 23-ft ladder leans against a building so that the angle between the ground and the ladder is 80°. How high does the ladder reach up the side of the building?
If the ladder is lean against the TOP of the building and the building is vertically standing above the ground, we can use the sine function to solve this question. That is the heigh of the building is
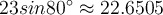
If the ladder is NOT lean against the TOP of the building and the building is vertically standing above the ground, then the height we just calculated is just a portion of the building and it represents where the ladder reach up the side of the building.
1/04/2023
How can De Moivre's theorem be described? What is the scope of this theorem? Examples for roots and powers.
Finding powers of complex numbers is greatly simplified using De Moivre’s Theorem.
According to the De Moivre’s Theorem
If Z = r(cos θ + isin θ) is a complex number, then Zn = rn[cos(nθ) + isin(nθ)]
where n is a positive integer. Zn = rn cis(nθ)
How does it come from? To understand this theorem, we must know the products of complex numbers in polar form and the quotients of complex numbers in polar form first.
Recall that :
sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
sin(α – β) = sin(α)cos(β) – cos(α)sin(β)
cos(α + β) = cos(α)cos(β) – sin(α)sin(β)
cos(α – β) = cos(α)cos(β) + sin(α)sin(β)









![(1+ \sqrt[]{3}i)^3 (1+ \sqrt[]{3}i)^3](https://my.uopeople.edu/filter/tex/pix.php/e2a1aa6d30a021d4041e05b48fbfd819.png)
![r= \sqrt[]{ 1^{2}+( \sqrt[]{3})^2 } =2 r= \sqrt[]{ 1^{2}+( \sqrt[]{3})^2 } =2](https://my.uopeople.edu/filter/tex/pix.php/27e227ed3f7354581e815bbd29ef736c.png)
![tan \theta= \sqrt[]{3} tan \theta= \sqrt[]{3}](https://my.uopeople.edu/filter/tex/pix.php/fbaaa49376a34eac20e70354b2af50f2.png)
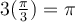
![(1+ \sqrt[]{3}i)^3=2^3(cos\pi +sin \pi)=-8 (1+ \sqrt[]{3}i)^3=2^3(cos\pi +sin \pi)=-8](https://my.uopeople.edu/filter/tex/pix.php/1655edd02ce67ad8bf191b7f102e190b.png)
![(\sqrt[]{2}+ \sqrt[]{2}i)^3 (\sqrt[]{2}+ \sqrt[]{2}i)^3](https://my.uopeople.edu/filter/tex/pix.php/5244302c0513b4819db33055eb6006d4.png)
![r= \sqrt[]{ (\sqrt[]{2})^{2}+( \sqrt[]{2})^2 } =2 r= \sqrt[]{ (\sqrt[]{2})^{2}+( \sqrt[]{2})^2 } =2](https://my.uopeople.edu/filter/tex/pix.php/e7ea7073eb6dfd20d2e687675801f89c.png)
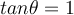
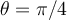
![(\sqrt[]{2}+ \sqrt[]{2}i)^3=2^3(cos3\pi/4 +sin3\pi/4)=\sqrt[]{2}(-4+4i) (\sqrt[]{2}+ \sqrt[]{2}i)^3=2^3(cos3\pi/4 +sin3\pi/4)=\sqrt[]{2}(-4+4i)](https://my.uopeople.edu/filter/tex/pix.php/27fa86cc1df32ea30b7bb303ec26f482.png)
![(1+ \sqrt[]{3}i)^{ \frac{1}{2}} (1+ \sqrt[]{3}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/0bcf834417249adadad03ab63b80f781.png)
![r= \sqrt[]{(1)^2+ (\sqrt[]{3})^2 } =2 r= \sqrt[]{(1)^2+ (\sqrt[]{3})^2 } =2](https://my.uopeople.edu/filter/tex/pix.php/b6c6ab4a7d3b72a4e501344b3878d9b4.png)
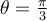
![(1+ \sqrt[]{3}i)^{ \frac{1}{2}} (1+ \sqrt[]{3}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/bc652a167de562231e4bfc6650ced7c8.png)
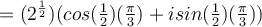
![\sqrt[]{2} ( \frac{\sqrt[]{3}}{2} + \frac{1}{2} i) \sqrt[]{2} ( \frac{\sqrt[]{3}}{2} + \frac{1}{2} i)](https://my.uopeople.edu/filter/tex/pix.php/05204267c26b6e10307752acfdad22f2.png)
![(\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}} (\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/c683ac0c2924fca4c2c086cb12a6ccc0.png)
![r= \sqrt[]{( \sqrt[]{2})^2+(\sqrt[]{2})^2} =2 r= \sqrt[]{( \sqrt[]{2})^2+(\sqrt[]{2})^2} =2](https://my.uopeople.edu/filter/tex/pix.php/e4ce902d69d67877998263642c396dfd.png)
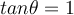
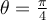
![(\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}} (\sqrt[]{2}+ \sqrt[]{2}i)^{ \frac{1}{2}}](https://my.uopeople.edu/filter/tex/pix.php/39deff4f37e68a7f4336999997dfcc1d.png)
![= \sqrt[]{2}(cos \frac{ \pi }{8} +isin \frac{ \pi }{8})= \sqrt[]{2}( \sqrt[]{\frac{1+ \frac{\sqrt[]{2}}{2} }{2} } +\sqrt[]{\frac{2-\sqrt[]{2} }{2} }) = \sqrt[]{2}(cos \frac{ \pi }{8} +isin \frac{ \pi }{8})= \sqrt[]{2}( \sqrt[]{\frac{1+ \frac{\sqrt[]{2}}{2} }{2} } +\sqrt[]{\frac{2-\sqrt[]{2} }{2} })](https://my.uopeople.edu/filter/tex/pix.php/1de22172a25f5ea46614d04c2f59681f.png)


